A self-affine tile is a two-dimensional set satisfying an expansion identity that allows tiling images to be generated. In this article, we discuss the generation of such images paying particular attention to the boundary of the set, which frequently displays a fractal structure. Read More »
Motivated by the excellent work of Bill Davis and Jerry Uhl’s Differential Equations & Mathematica [1], we present in detail several little-known applications of the fast discrete Fourier transform (DFT), also known as FFT. Namely, we first examine the use of the FFT in multiplying univariate polynomials and integers and approximating polynomials with sines and cosines (also known as the fast Fourier fit or FFF). We then examine the use of the FFF in solving differential equations with Laplace transforms and rediscovering trigonometric identities. Read More »
In this article we examine three well-known problems from the recreational mathematics literature dealing with goal-oriented strategies set on a discrete state space. We use the backtrack paradigm to implement an exhaustive search and deduce some theoretical results, which in some cases allows us to provide an explicit description of their solutions. Read More »
It has long been known that Buffon’s needle experiments can be used to estimate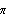 
. Three main factors influence these experiments: grid shape, grid density, and needle length. In statistical literature, several experiments depending on these factors have been designed to increase the efficiency of the estimators of 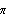and to use all the information as fully as possible. We wrote the package BuffonNeedle to carry out the most common forms of Buffon’s needle experiments. In this article we review statistical aspects of the experiments, introduce the package BuffonNeedle, discuss the crossing probabilities and asymptotic variances of the estimators, and describe how to calculate them using Mathematica. Read More »
Automated braking system design relies on knowledge of how tire friction varies with the depth of the skid. This knowledge is captured empirically in the tire mu slip curve. An extended Kalman filter is designed to fit test data to the mu slip curve. An animation of the Kalman filter’s convergence is presented. Read More »
This article proposes a new symbolic technique for offshore design technology. Several solutions deal with the design of longitudinally elastic offshore constructions. Details are discussed for a drillstem and a riser. Both symbolic and numerical solutions derived with Mathematica are applied to solve problems in offshore design technology. All symbolic approaches are based on solutions of the linear boundary problems that arise. Additionally, a new symbolic solution for the generic boundary problem is discussed in detail. Read More »
NB
