The special function ![]() (the Walker function) and its derivatives are important for the description of near-wall turbulent flows. This article gives exact expressions for these functions, based on original identities for the hypergeometric functions
(the Walker function) and its derivatives are important for the description of near-wall turbulent flows. This article gives exact expressions for these functions, based on original identities for the hypergeometric functions ![]() and
and ![]() . We also introduce a new initial value problem that generates interpolating functions for
. We also introduce a new initial value problem that generates interpolating functions for ![]() and its derivatives.<\p>
and its derivatives.<\p>
Introduction
The quantitative description of turbulent flows is known to be severely hampered by the extremely rapid variations in the mean and higher-order statistics in the near-wall region. Some very early studies [1, 2, 3] showed that the basic structure of an attached turbulent boundary layer consists of a viscous wall layer, in which the turbulent and laminar stresses are of comparable magnitude, and a defect layer, in which the velocity profile may be expressed in terms of a small perturbation to the external flow solution [4]. Also, [1, 2, 3] showed that this structure naturally leads to a universal velocity solution that has logarithmic behavior and depends on the velocity and length scales based on the friction velocity.
For separated flows, this picture changes dramatically; the friction velocity reduces to zero, so that a new scaling procedure based on the local pressure gradient at the wall needs to be introduced. The logarithmic solution is then reduced to a square-root velocity profile. Aspects of the complex flow structure due to separation are thoroughly discussed in [4].
To incorporate the structure of organized motion into a near-wall analytical model, Walker et al. [5] proposed a time-dependent formulation based on the dynamical features of the wall layer. Following the general description commonly found in the literature, the flow dynamics are considered to be dominated by two features: wall layer streaks and the bursting phenomenon. The streaks are elongated in the flow direction, with length of the order of ![]() (where
(where ![]() ,
, ![]() is the kinematic viscosity, and
is the kinematic viscosity, and ![]() is the friction velocity), and can be observed over a large characteristic time, the quiescent period [6].
is the friction velocity), and can be observed over a large characteristic time, the quiescent period [6].
Analytical near-wall solutions for turbulent flows are of central significance, since the extreme thinness of the viscous sublayer naturally demands the use of exceptionally fine meshes in the numerical computation of problems of practical relevance. This difficulty can be naturally overcome, provided the local analytical solutions are used to bridge the viscous-dominated region.
In [5], the duration of the quiescent period is assumed to be much larger than the duration of the bursting process, so that solutions for the unsteady Navier-Stokes equations can be given in terms of the flow development between pairs of streaks. The analysis resorts to standard methods for orthogonal functions to arrive at a set of three nonlinear governing equations that have to be solved numerically. In addition, a semi-similarity procedure is proposed, resulting in a solution that includes ![]() . This function is a similarity solution of the linear diffusion equation that behaves logarithmically for large
. This function is a similarity solution of the linear diffusion equation that behaves logarithmically for large ![]() and vanishes at
and vanishes at ![]() . Mean velocity profiles are obtained by evaluating a time-average of the solution over the period between bursts,
. Mean velocity profiles are obtained by evaluating a time-average of the solution over the period between bursts, ![]() .
.
In mathematics ![]() is generally used to denote a variant of the Riemann zeta function. Here, no confusion should arise: the function
is generally used to denote a variant of the Riemann zeta function. Here, no confusion should arise: the function ![]() , as defined in [5], is given by the equation e1 below.
, as defined in [5], is given by the equation e1 below.
Instantaneous and averaged velocity profiles are presented for four combinations of ![]() (the dimensionless pressure gradient parameter) and
(the dimensionless pressure gradient parameter) and ![]() in accordance with typically measured values. For constant pressure flow (
in accordance with typically measured values. For constant pressure flow (![]() ,
, ![]() ), the canonical boundary layer structure is well reproduced. Under a favorable pressure gradient (
), the canonical boundary layer structure is well reproduced. Under a favorable pressure gradient (![]() ,
, ![]() ), the instantaneous profiles are accelerated as expected. For adverse pressure gradients (
), the instantaneous profiles are accelerated as expected. For adverse pressure gradients (![]() ,
, ![]() ;
; ![]() ,
, ![]() ),
), ![]() decreases and, for the latter case, reverse instantaneous flow is observed over the latter part of the cycle.
decreases and, for the latter case, reverse instantaneous flow is observed over the latter part of the cycle.
Here, we develop a new version of the near-wall turbulent velocity profile shown in [5], in particular, of the ![]() function. This article introduces the required features of function
function. This article introduces the required features of function ![]() and its derivatives. In addition, we present some original identities for the hypergeometric functions
and its derivatives. In addition, we present some original identities for the hypergeometric functions ![]() and
and ![]() .
.
Identity Involving  and
and 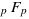
The function ![]() is of particular relevance, being the only known similarity solution of the linear diffusion equation that behaves logarithmically for large
is of particular relevance, being the only known similarity solution of the linear diffusion equation that behaves logarithmically for large ![]() and vanishes at
and vanishes at ![]() [5].
[5].
The ![]() function can be defined either in terms of an expansion or an integral, as shown in [5] (equations (44) and (42)). In the latter form, the triple integral can be rearranged to a single integral.
function can be defined either in terms of an expansion or an integral, as shown in [5] (equations (44) and (42)). In the latter form, the triple integral can be rearranged to a single integral.
![]()
![]()
The coefficients ![]() are defined by a recurrence relation.
are defined by a recurrence relation.
![]()
The sum in e1 is uniformly convergent for all ![]() . This is particularly useful in the evaluation of
. This is particularly useful in the evaluation of ![]() for small to moderate values of
for small to moderate values of ![]() [5].
[5].
This solves the recurrence equation.
![]()
![]()
FullSimplify shows that the coefficients ![]() are the harmonic numbers.
are the harmonic numbers.
![]()
![]()
After substituting equation e4 into equation e1, the sum turns out to be a hypergeometric function.
![]()

This is the second term of e5.
![]()
![]()
This is difficult to calculate for large numerical values of ![]() , because
, because ![]() is extremely small, while the hypergeometric function is extremely large. To remove
is extremely small, while the hypergeometric function is extremely large. To remove ![]() from
from ![]() , we use the following identity.
, we use the following identity.
![]()
![]()
Take the derivative of e6 with respect to ![]() for
for ![]() and
and ![]() .
.
![]()
![]()
Use e7 to substitute into e5.
![]()
![]()
To verify that e8 is an identity, we evaluate its right-hand side for ![]() with 100 digits of precision.
with 100 digits of precision.
![]()
![]()
![]()
![]()
For ![]() and
and ![]() , Mathematica 8 gives the following.
, Mathematica 8 gives the following.
![]()
![]()
![]()
![]()
Mathematica 8 can evaluate e9 and e10 for numerical values of ![]() . The following rule generates derivatives of order n that earlier versions of Mathematica can evaluate.
. The following rule generates derivatives of order n that earlier versions of Mathematica can evaluate.
![]()
For ![]() and
and ![]() , the function WalkerDerivative gives the following.
, the function WalkerDerivative gives the following.
![]()

![]()

To verify that the right-hand sides of e9 and e11 are equal and that the right-hand sides of e10 and e12 are equal, we evaluate them for ![]() with 100 digits of precision.
with 100 digits of precision.
![]()
![]()
Initial Value Problem
To derive the initial value problem for ![]() , we use e8 and its derivatives.
, we use e8 and its derivatives.
![]()
![]()
![]()
![]()
![]()
![]()
To obtain the desired initial value problem, we eliminate from e14 and e15 the hypergeometric function and replace ![]() by 0 in e13 and e14.
by 0 in e13 and e14.
![]()
![]()
The resulting ordinary differential equation is equivalent to equations (40) and (41) in [5]. The condition ![]() is also given in [5]. However, the condition
is also given in [5]. However, the condition ![]() is missing in [5], where no attempt is made to obtain a numerical solution.
is missing in [5], where no attempt is made to obtain a numerical solution.
We plot the function ![]() (blue) and its derivative
(blue) and its derivative ![]() (purple).
(purple).


Conclusion
Exact expressions for the Walker function ![]() and its derivatives are obtained. From a computational point of view, an important result is the specification of the initial value problem, for it allows extremely fast interpolating functions to be generated. From a mathematical point of view, some new identities between the two hypergeometric functions
and its derivatives are obtained. From a computational point of view, an important result is the specification of the initial value problem, for it allows extremely fast interpolating functions to be generated. From a mathematical point of view, some new identities between the two hypergeometric functions ![]() and
and ![]() are presented. These identities were revealed by the built-in Mathematica functions RSolve, Sum, and FullSimplify. Of possible interest is the application of the techniques to discover new identities and to the problems described in the book by Petkovšek et al. [7].
are presented. These identities were revealed by the built-in Mathematica functions RSolve, Sum, and FullSimplify. Of possible interest is the application of the techniques to discover new identities and to the problems described in the book by Petkovšek et al. [7].
Acknowledgments
The first author is thankful to the Brazilian National Research Council (CNPq) and the Brazilian National Institute of Standards (INMETRO) for their financial support of this research through a CNPq Research Fellowship-Edital MCT/CNPq/Inmetro nº 059/2010-PROMETRO Processo Nº 563061/2010-3.
The second author is grateful to the Brazilian National Research Council (CNPq) for the award of a Research Fellowship (Grant No. 303982/2009-8). The work was financially supported by the Rio de Janeiro Research Foundation (FAPERJ) through Grant E-26/170.005/2008.
References
| [1] | L. Prandtl, “Über die ausgebildete Turbulenz,” ZAMM: Journal of Applied Mathematics and Mechanics/Zeitschrift für Angewandte Mathematik und Mechanik, 5, 1925 pp. 136-139. |
| [2] | T. von Kármán, “Mechanische Aehnlichkeit und Turbulenz,” Proceedings of the Third International Congress for Applied Mechanics, Vol. 1, Stockholm, 1930 (C. W. Oseen and W. Weibull, eds.), Stockholm: AB. Sveriges Litografiska Tryckerier, 1931 pp. 79-93 (in German). |
| [3] | C. B. Millikan, “A Critical Discussion of Turbulent Flow in Channels and Circular Tubes,” Proceedings of the 5th International Congress for Applied Mechanics, Cambridge, MA, 1938, New York: Wiley, 1939 pp. 386-392. |
| [4] | J. B. R. Loureiro, A. P. Silva Freire, “Scaling of Turbulent Separating Flows,” International Journal of Engineering Science, 49(5), 2011 pp. 397-410. doi:10.1016/j.ijengsci.2010.12.001. |
| [5] | J. D. A. Walker, D. E. Abbott, R. K. Scharnhorst, and G. G. Weigand, “Wall-Layer Model for the Velocity Profile in Turbulent Flows,” American Institute of Aeronautics and Astronautics Journal, 27(2), 1989 pp. 140-149. |
| [6] | S. J. Kline, W. C. Reynolds, F. A. Schraub, and P. W. Rundstadler, “The Structure of Turbulent Boundary Layers,” Journal of Fluid Mechanics, 30(4), 1967 pp. 741-773. journals.cambridge.org/abstract_S0022112067001740. |
| [7] | M. Petkovšek, H. S. Wilf, D. Zeilberger, A=B, Wellesley, MA: A. K. Peters, 1996. www.cis.upenn.edu/~wilf/AeqB.html. |
| M. D. Mikhailov and A. P. Silva Freire, “The Walker Function,” The Mathematica Journal, 2012. dx.doi.org/doi:10.3888/tmj.14-11. | |
About the Authors
M. D. Mikhailov
INMETRO—Divisão de Metrologia em Dinâmica de Fluidos
Dimci/Dinam, Prédio 3, Av. Nossa Senhora das Graças 50
Duque de Caxias, 25250-020
Rio de Janeiro, Brasil
m.d.mikhailov@gmail.com
Atila P. Silva Freire
Mechanical Engineering Program (PEM/COPPE/UFRJ)
C.P. 68503, 21941-972
Rio de Janeiro, Brazil
atila@mecanica.coppe.ufrj.br