In this article we examine three well-known problems from the recreational mathematics literature dealing with goal-oriented strategies set on a discrete state space. We use the backtrack paradigm to implement an exhaustive search and deduce some theoretical results, which in some cases allows us to provide an explicit description of their solutions.
The Problem of the Buckets
Jack and Jill went up the hill,
To fetch a pail of water;
Jack fell down and broke his crown,
and Jill came tumbling after.Nursery Rhyme
J. W. Elliot, 1765
Consider the following question. Given two unmarked buckets of capacities 3 and 5 liters, how can we obtain exactly 1 liter of water from an inexhaustible well? The answer is to fill the 3-liter bucket first and empty it into the other bucket. Then, refill the 3-liter bucket from the well and use it to completely fill the other one, leaving the 1 liter desired. This problem is one of a famous category of “decanting” problems that have always appealed to a wide audience, including recreational mathematicians and computer scientists. Similar problems have found valuable applications in the analysis and teaching of algorithmic techniques, typifying many of the difficulties involved in the design of goal-oriented strategies. In the problem of the buckets, it is easy to show that if we have buckets of capacities ![]() and
and ![]() liters, and we start with both empty, the problem is solvable if and only if
liters, and we start with both empty, the problem is solvable if and only if ![]() and
and ![]() are coprime. If this is the case, we have several ways to proceed. Each of them can be described by a sequence of ordered pairs accounting for the states through which we pass at each step towards our goal. Consider for instance, one of the shortest sequences that solves the problem for capacities 2 and 5: {{0, 0}, {0, 5}, {2, 3}, {0, 3}, {2, 1}}.
are coprime. If this is the case, we have several ways to proceed. Each of them can be described by a sequence of ordered pairs accounting for the states through which we pass at each step towards our goal. Consider for instance, one of the shortest sequences that solves the problem for capacities 2 and 5: {{0, 0}, {0, 5}, {2, 3}, {0, 3}, {2, 1}}.
In solving this problem we notice that any proper move we can make at each step is one of three types:
- Fill an empty bucket from the well. We do not fill a partially filled bucket because that wastes the moves that made it partially full.
- Empty a full bucket into the well.
- Pour one bucket into another, in such a way that we completely empty the first or fill the second.
The general ideas in solving these types of problems are as follows. There is a starting state and one or more final states that we aim to reach. If we are able to do so, we then want to have a description of the actual paths taken from the start to each one of the final states; moreover, we want those paths of minimal length. In order to direct a current partial path towards the goal, we follow guidelines that help to avoid entering blind alleys or performing wasteful moves. For instance, we should avoid reaching a previously visited state. In general, an explicit list describing all the traversed states to the goal would suffice, upgrading an upper bound on the length of future solution paths to alleviate the phenomenon of combinatorial explosion that this approach entails. A “Markovian” point of view is often adopted; the choice of the next state only depending on the current one, and not on the history of all or any previous ones. We can thus encapsulate the process of a single change of state by using the following list of productions. Note the conditionals appearing in the last two productions; without them we might, in certain cases, stay in the same current state.
![]()
We use the function ReplaceList to gather all possible next states.
![]()
For example, if we have managed to get to state ![]() in our first example, the states we can then access are computed as:
in our first example, the states we can then access are computed as:
![]()
![]()
That is, we could empty the first bucket by either pouring its content into the well or into the other bucket. Note that this list of candidates is returned in lexicographic order.
From the computational point of view, a good approach to solving this kind of problem is to use the backtrack technique. Backtrack is a basic method in the computer scientist repertoire, often used in problems in which it is required to find all solutions satisfying a given property. The general framework is that of a selection of all finite paths traversing a (possibly infinite) discrete state space. By its exhaustive nature, backtrack is often modified in order to overcome large time constraints that are typically exponential in nature (not so its space restrictions, which are always relatively affordable) [1]. However, its popularity arises mainly due to its straightforward quality and simplicity in solving an extensive class of computational problems. Often the main reason for choosing backtrack is simply the fact that, for many important problems, there is no other feasible approach discovered so far. It is our aim in this article to illustrate an interesting instance of such problems and, in the process, to show how the general backtrack method can be modified in an ad-hoc way, leading to a significant improvement in execution time. This tailoring can arise from some theoretical insight or from a study of the computational burden imposed by its particular use. In general, the backtrack method is sufficiently flexible to give the programmer considerable scope in exercising skills for solving important combinatorial problems in an effective way.
Although there have been efforts in providing general backtrack routines—notably those included in Skiena’s excellent books [2, 3], the value of backtrack lies not in its generality per se but in its capacity of adaptation. Because of drawbacks in the languages implementing it, its role has been largely overlooked. In fact, there was a time when the recursive style of programming was discouraged on the grounds that it was “unnatural.” The truth was that what was unnatural were the features of the primitive programming languages available.
In its more general setup, the backtrack mechanism grows a currently acceptable partial result ![]() by choosing from a set of candidates
by choosing from a set of candidates ![]() , gathered by a function such as the function nextStates. Each element of
, gathered by a function such as the function nextStates. Each element of ![]() is successively appended to
is successively appended to ![]() and the process is recursively iterated with each of these new partial results. This growing either leads to the finding of a solution or to a stage in which
and the process is recursively iterated with each of these new partial results. This growing either leads to the finding of a solution or to a stage in which ![]() is void, in which case we backtrack to consider another candidate instead of the last one appended. By repeating this process we arrive at fully spanning the whole state space in a goal-oriented and efficient way; however, as we mentioned before, on occasion this is not enough to counterbalance a potential combinatorial explosion. The following pseudocode implements this idea.
is void, in which case we backtrack to consider another candidate instead of the last one appended. By repeating this process we arrive at fully spanning the whole state space in a goal-oriented and efficient way; however, as we mentioned before, on occasion this is not enough to counterbalance a potential combinatorial explosion. The following pseudocode implements this idea.
backtrack[r] If r is a solution Print[r] and stop Compute S Map[backtrack[Append[r,#]]&, S]
So our query for a solution would be ![]() . We can easily modify this scheme to search for all possible solutions, thus attempting to find the “best one” in an exhaustive manner. By its very nature, backtrack allows us to prune the branches of the tree spanned by this traversal in a systematic way, thus cutting unfeasible branches as soon as possible, which, in a full searching of the global state space results is vital.
. We can easily modify this scheme to search for all possible solutions, thus attempting to find the “best one” in an exhaustive manner. By its very nature, backtrack allows us to prune the branches of the tree spanned by this traversal in a systematic way, thus cutting unfeasible branches as soon as possible, which, in a full searching of the global state space results is vital.
The following function ![]() computes the solution list corresponding to the problem of obtaining 1 liter with buckets of capacities
computes the solution list corresponding to the problem of obtaining 1 liter with buckets of capacities ![]() and
and ![]() liters, limiting the exhaustive search to a depth
liters, limiting the exhaustive search to a depth ![]() . When
. When ![]() , it returns the empty list.
, it returns the empty list.

We verify our original example.
![]()
![]()
The following is a table of the length of the solutions corresponding to all possible combinations of the values ![]() and
and ![]() of at most size 21. Note that we still do not have a bound on the number of steps taken, so we use
of at most size 21. Note that we still do not have a bound on the number of steps taken, so we use ![]() for all cases; as the matrix
for all cases; as the matrix ![]() is symmetric with zeroes on the main diagonal, the computing time can be shortened.
is symmetric with zeroes on the main diagonal, the computing time can be shortened.


Enlarging the possible size of the buckets and assigning a cherry tone to the length of the solutions leads to the following picture.


Note that the values on the first row and columns account for the solutions ![]() and
and ![]() . The bands of 2s above and below the main diagonal establish the solutions
. The bands of 2s above and below the main diagonal establish the solutions ![]() and
and ![]() .
.
Perhaps the reader will find it interesting to prove that, if ![]() is an integer and
is an integer and ![]() , then
, then ![]() . What strategy does this result imply? What happens in the case when
. What strategy does this result imply? What happens in the case when ![]() is an integer?
is an integer?
Note that the longest entry in the previous matrix corresponds to the case ![]() ,
, ![]() (or vice versa) of length 36.
(or vice versa) of length 36.
![]()

Inspection of this list suggests an easy procedure to solve the case where ![]() is odd and
is odd and ![]() (they will always be coprime because a linear combination of them, namely
(they will always be coprime because a linear combination of them, namely ![]() , equals 1). The length in this case will be equal to
, equals 1). The length in this case will be equal to ![]() .
.
The next function helps to visualize the entire state space involved in solving the problem of the buckets. We associate a labeled disk with each state ![]() and place them at the vertices of a regular polygon. We draw an arrow from state
and place them at the vertices of a regular polygon. We draw an arrow from state ![]() to state
to state ![]() if state
if state ![]() can be reached from state
can be reached from state ![]() . The following function sG computes the resulting graphic object.
. The following function sG computes the resulting graphic object.

Here is the graph for buckets of capacities 2 and 5. Can the reader follow the path describing our previous solution? Note also that some states, like 11, are inaccessible.
![]()

In the case ![]() ,
, ![]() , the following graph shows that the goal states are inaccessible from 00. In fact this graph is the superposition of two graphs formed by those states reachable and unreachable from 00.
, the following graph shows that the goal states are inaccessible from 00. In fact this graph is the superposition of two graphs formed by those states reachable and unreachable from 00.
![]()

A Bouquet of Buckets
The following code generalizes our problem to that of obtaining 1 liter from handling a number of buckets of given capacities.

For instance, with three buckets of capacities 3, 11, and 20, the steps necessary to obtain 1 liter are as follows.
![]()
![]()
Some problems are more time-consuming than others.
![]()
![]()
The capacity of the extra buckets can substantially affect this timing.
![]()
![]()
Having an extra bucket might not be useful in shortening the solution.
![]()
![]()
![]()
But sometimes it does.
![]()
![]()
A better choice would be the following.
![]()
![]()
So, given a set of buckets, what would be the best choice if we are allowed to add one new bucket to the set? Our aim would be to obtain the shortest solution possible. Note that there is a maximum capacity for this new bucket beyond which we cannot shorten the solution any further. For example, if we start with buckets of capacities 2 and 7, adding a bucket of capacity 3 provides the shortest solution (the other two solutions are buckets of capacities 6 or 8); choosing a capacity greater than 17 is equivalent to using only the two original buckets. Our previous longest case ![]() ,
, ![]() would greatly benefit from the addition of an extra bucket of capacity 18. In general, looking at the previous matrix B we conclude that the addition of a bucket of capacity
would greatly benefit from the addition of an extra bucket of capacity 18. In general, looking at the previous matrix B we conclude that the addition of a bucket of capacity ![]() substantially speeds up the process that starts with two buckets of capacities
substantially speeds up the process that starts with two buckets of capacities ![]() ,
, ![]()
![]() .
.
There are many fascinating variants of the problem of the buckets and we recommend references [4, 5]. They address problems like the following: we are given a filled vessel of capacity 12 and two empty vessels of capacities 9 and 5. How can we divide the liquid into two equal portions? By traversing paths in a network of equilateral triangles, a solution (or its absence) is found for the case of three jugs.
The Problem of the Toads and the Frogs
The clever men at Oxford
Know all that is to be knowed.
But none of them knows half as much
As intelligent Mr. Toad!The Wind in the Willows
Kenneth Grahame, 1908
The Problem of the Buckets introduced in the previous section deals with traversing a state space and solving the problem of finding the shortest route connecting two particular nodes in this space. The problem here considers the same traversal, but with a different goal, providing an interesting new background from which to deduce properties that this time allows us to explicitly describe an optimal strategy.
Consider the Problem of the Toads and the Frogs: ![]() toads and
toads and ![]() frogs are placed in a linear grid of
frogs are placed in a linear grid of ![]() squares. The toads are arranged in the first
squares. The toads are arranged in the first ![]() squares and the frogs in the last
squares and the frogs in the last ![]() squares, each pet facing each other with a single vacancy in between as depicted in Figure 1. From this initial configuration our problem is to transfer all toads to where the frogs are and vice versa by means of two kinds of movements performed sequentially by a single pet at a time; moreover, we want the fastest way of achieving this. Any pet can only move to the empty space if it happens to be next to it; if this is not the case, it can jump in the direction it is facing over an adjacent pet regardless of its type, provided that the empty space is at the square it lands on. At all times the process is performed within the limits of the squares. The movements resemble those in the game of checkers, but without any piece removal. Denoting a toad by T, a frog by F, and the empty space by an underscore _, we can describe a solution to the problem in Figure 1 by the following sequence of states, where an arrow indicates a transition to the next state:
squares, each pet facing each other with a single vacancy in between as depicted in Figure 1. From this initial configuration our problem is to transfer all toads to where the frogs are and vice versa by means of two kinds of movements performed sequentially by a single pet at a time; moreover, we want the fastest way of achieving this. Any pet can only move to the empty space if it happens to be next to it; if this is not the case, it can jump in the direction it is facing over an adjacent pet regardless of its type, provided that the empty space is at the square it lands on. At all times the process is performed within the limits of the squares. The movements resemble those in the game of checkers, but without any piece removal. Denoting a toad by T, a frog by F, and the empty space by an underscore _, we can describe a solution to the problem in Figure 1 by the following sequence of states, where an arrow indicates a transition to the next state:
TT_FF → T_TFF → TFT_F → TFTF_ → TF_FT →_FTFT → F_TFT → FFT_T → FF_TT.

Figure 1. The Problem of the Toads and the Frogs for the case ![]() .
.
In order to describe a solution, we can regard each stage as a movement of the vacant square; this allows us to unambiguously recover the positions of all the pets at each stage and focus on the essential characteristics of the problem. Let us denote jumps to the left and right and moves to the left and right performed by the empty square by the digits 1, 2, 3, and 4, respectively (see Figure 2). Then the solution previously given for the case ![]() can be described more concisely by the word 32411423, or equivalently as
can be described more concisely by the word 32411423, or equivalently as ![]() , where we use powers to denote repetitions of the same sequence. We will also denote this process as
, where we use powers to denote repetitions of the same sequence. We will also denote this process as ![]() .
.

Figure 2. The movements of the toads and frogs can be interpreted as movements of the empty cell according to this code.
Let us make the following observations.
- If w is a solution, then
 is also a solution.
is also a solution. - In any minimum-length solution, the symbols 1 and 2 and the symbols 3 and 4 cannot appear together. This condition is, however, not sufficient. The solution 1423142323132 for the case
 complies with it even though it is not of minimal length.
complies with it even though it is not of minimal length. - Despite appearances,
 , that is, performing movement 1 and then movement 4 is not equivalent to performing movement 3. Similarly,
, that is, performing movement 1 and then movement 4 is not equivalent to performing movement 3. Similarly,  . If we denote by
. If we denote by 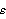 the empty word (equivalent to “do nothing”), we have
the empty word (equivalent to “do nothing”), we have  ,
,  ,
,  ,
,  and
and  .
. - Any solution can be made to contain only the digits 2 and 3 or only the digits 1 and 4. This comes from the identities
 ,
,  ,
,  ,
, 
but their presence helps in the shortening of solutions.
We consider now the following productions corresponding to each of the movements of the empty space.
![]()
Function toadsAndFrogs takes a string describing a starting state and attempts to find a solution to the problem of swapping the positions of the frogs and toads. As in the Problem of the Buckets, it makes use of backtrack to traverse the state space up to a given depth.

For instance, for the problem depicted in Figure 1 we obtain the actual sequence with the coding of the movements of the empty space involved as follows.
![]()
![]()
We can compute a table comprising all solutions for each one of the members of the state space.
![]()

Amphibia in Theory
Unlike the space of buckets, the Problem of the Toads and Frogs has an extensive state space including ![]() states, in which any state can be reached from any other one. Specifically, let
states, in which any state can be reached from any other one. Specifically, let ![]() be the set of all possible configurations of
be the set of all possible configurations of ![]() toads and
toads and ![]() frogs. Then the following property applies.
frogs. Then the following property applies.
![]()
(We use the symbol ![]() to indicate end of proof.)
to indicate end of proof.)
Note that this proof does not provide a way to obtain the shortest sequence we seek.
We need to apply words describing moves to configurations of toads and frogs. These words are juxtapositions of powers of symbols taken from the set {1, 2, 3, 4}, the powers being used as a shorthand to indicate repetitions of their respective base. Words will be described by a list of pairs similarly as those expressing the canonical factorization of a positive integer number. Because these words grow quite rapidly, we will work with them factorized, their type being ![]() . For example, if
. For example, if ![]() , the transformation mentioned in the previous proof will be structured as
, the transformation mentioned in the previous proof will be structured as ![]() . States will have the type
. States will have the type ![]() , where each of their members will be one of “T”, “F”, or “_” and only one occurrence of the underscore is allowed and required. Their action by a word will be computed by the function action. In order to display patterns and words more concisely, we use predicates showPattern and showWord (for an alternative way regarding the design of the latter, see [6]).
, where each of their members will be one of “T”, “F”, or “_” and only one occurrence of the underscore is allowed and required. Their action by a word will be computed by the function action. In order to display patterns and words more concisely, we use predicates showPattern and showWord (for an alternative way regarding the design of the latter, see [6]).

To verify our previous assertion we proceed as:
![]()
![]()
![]()
![]()
![]()
![]()
The word ![]() is used on our problem as follows.
is used on our problem as follows.
where X is such that
For example, the action of sequence ![]() on the case
on the case ![]() is:
is:
![]()
![]()
Denoting the reverse of ![]() by
by ![]() , we have the following result.
, we have the following result.

![]()
![]()
This result is used to recover from the effect of ![]() . For example:
. For example:
![]()
![]()
Unifying Theorems 2 and 3, we can explicitly solve our problem for the case of an equal number of pets.
![]()

Testing this result for the case ![]() we obtain:
we obtain:
![]()
![]()
The case where we have an unbalanced number of pets is more involved. First, we deduce the following result from Theorem 4.


![]()
stand for the previously introduced word ![]() after applying the transposition
after applying the transposition
![]()

![]()
![]()
![]()
![]()
We state Theorems 5 through 7 without their proofs, which are somewhat laborious. They progressively allow us to obtain an explicit word solving our general problem.
For example, for the case ![]() we have:
we have:
![]()
![]()
![]()
This case involves the action of families ![]() and
and ![]() together. Consider, for example, the following two cases.
together. Consider, for example, the following two cases.
![]()
![]()
![]()
![]()
Now we only need to consider word ![]() as given in the following theorem.
as given in the following theorem.

Examples covering each one of these four cases follow.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
We finally arrive at our main result.
Our results provide the word 3241423 to solve T_FFF and the word 32411423 to solve TT_FF, which we previously attacked exhaustively with the help of backtrack.
Using a different approach to reach a different aim, Berlekamp et al. [7] apply the theory of surreal numbers to analyze the Problem of Toads and Frogs.
The Problem of the Rabbits
Oh dear! Oh dear!
I shall be too late!The white rabbit in Alice in Wonderland
Lewis Carroll, 1865
Consider the following interesting variation of the Problem of the Toads and Frogs in the previous section. There are ![]() rabbits confined in a grid of size
rabbits confined in a grid of size ![]() . All rabbits are labeled sequentially and are initially arranged as shown in Figure 3, leaving only a left-most empty space labeled 0. They can jump and move as in the Problem of the Toads and Frogs. The Problem of the Rabbits consists of orchestrating the series of state changes needed to take the rabbits from positions
. All rabbits are labeled sequentially and are initially arranged as shown in Figure 3, leaving only a left-most empty space labeled 0. They can jump and move as in the Problem of the Toads and Frogs. The Problem of the Rabbits consists of orchestrating the series of state changes needed to take the rabbits from positions ![]() to positions
to positions ![]() in the shortest number of moves.
in the shortest number of moves.

Figure 3. The problem of the rabbits for the case ![]() . Although they are displayed here looking to the left, they are free to turn and jump about within the confines of their world.
. Although they are displayed here looking to the left, they are free to turn and jump about within the confines of their world.
Any state is reachable from any other and the search space grows rapidly with ![]() , which renders a trial-and-error approach impractical. The following function rabbits adapts our backtrack paradigm to this problem. Given the number
, which renders a trial-and-error approach impractical. The following function rabbits adapts our backtrack paradigm to this problem. Given the number ![]() of rabbits and the depth of search, it exhaustively looks for a solution. The coding that we follow is the same as the one adopted to describe the empty space in the previous section as depicted in Figure 2.
of rabbits and the depth of search, it exhaustively looks for a solution. The coding that we follow is the same as the one adopted to describe the empty space in the previous section as depicted in Figure 2.

For example, if there are two rabbits we obtain:
![]()
![]()
With three rabbits, the solution sequence grows as:
![]()
![]()
Compiling a table of solutions for the cases of up to five rabbits, we obtain:
![]()

To get some insight into the problem, consider the following results.
![]()

Although useful, this result gives a large upper bound for the solution. For instance, instead of the 21 movements required to get from 0123456 to 0654321, we need 43 by using Theorem 8. Just to appreciate the subtleties involved, let us consider the steps used in applying one of the shortest solutions 222311322231132223113:
![]()
If instead of describing the movement of the 0 marker, we explicitly mention the label of the rabbit that has to move/jump, we have the following result.

This provides sequence ![]() as a 21-step solution for the case
as a 21-step solution for the case ![]() . In general, it provides a sequence significantly smaller than the one given by Theorem 8.
. In general, it provides a sequence significantly smaller than the one given by Theorem 8.
Once the training of our rabbits is over, they can be put in a circular board connecting the last square to the first one to study their reactions to a more difficult setup. This new arrangement is reflected in the following list of transformations that gives rise to the following function Crabbits (circular rabbits).
![]()

The results for up to six rabbits are:
![]()

Let us note that the symbol “0” in the previous transformation move is not really necessary. In looking at the resulting 0-less transformations for the first time, who would realize that these strange transformations correspond to movements performed by rabbits in a circular one-dimensional board!
Acknowledgments
This work was completed while the author was a visiting scholar at Wolfram Research, Inc., whose assistance and enthusiastic support is gratefully acknowledged. I would also like to thank the University of Queretaro in Mexico for their continued support.
References
| [1] | D. E. Knuth, “Estimating the Efficiency of Backtrack Programs” in Selected Papers on the Analysis of Algorithms, Stanford, CA: CSLI Publications, 2000, pp. 55-75. |
| [2] | S. S. Skiena, The Algorithm Design Manual, New York: Springer-Verlag, 1997. |
| [3] | S. S. Skiena, Implementing Discrete Mathematics: Combinatorics and Graph Theory in Mathematica, Reading, MA: Addison-Wesley, 1990. |
| [4] | H. S. M. Coxeter and S. L. Greitzer, Geometry Revisited, Washington, DC: The Mathematical Association of America, 1967. |
| [5] | T. H. O’Beirne, “Jug and Bottle Department,” in Puzzles and Paradoxes, New York: Oxford University Press, 1965 pp. 49-75. |
| [6] | P. Abbott, ed., “Tricks of the Trade,” The Mathematica Journal, 6(4), Fall 1996, pp. 17-26. |
| [7] | E. R. Berlekamp, J. H. Conway, and R. Guy, Winning Ways: For Your Mathematical Plays, Vol. 2, London: Academic Press, 1982. |
| J. Rangel-Mondragón, “Buckets and Jumping Pets,” The Mathematica Journal, 2011. dx.doi.org/doi:10.3888/tmj.11.1-3. | |
About the Author
Jaime Rangel-Mondragón received M.Sc. and Ph.D. degrees in applied mathematics and computation from the University College of North Wales in Bangor, UK. He has been a visiting scholar at Wolfram Research, Inc. and held research positions in the Faculty of Informatics at UCNW, the College of Mexico, the Center of Research and Advanced Studies, the Monterrey Institute of Technology, the Queretaro Institute of Technology, and the University of Queretaro in Mexico, where he is presently a member of the Faculty of Informatics. A prolific contributor to MathSource, he currently writes the column Geometric Themes for the Mathematica in Education and Research journal. His research interests include recreational mathematics, combinatorics, the theory of computing, computational geometry, and functional languages.
Jaime Rangel-Mondragón
Universidad Autónoma de Querétaro
Mexico
jrangelmondragon@gmail.com