Some extensions of Hamiltonian tours are explored.
The Original Icosian Game
In 1857 Sir William Rowan Hamilton invented the Icosian game [1]. In a world based on the dodecahedral graph, a traveler must visit 20 cities, without revisiting any of them. Today, when the trip makes a loop through all the vertices of the graph, it is called a Hamiltonian tour (or cycle). When the first and last vertices in a trip are not connected, it is called a Hamiltonian path (or trail). The first image shown is a tour; the second is a path.


Hamiltonian cycles gained popularity in 1880, when P. G. Tait made the conjecture: “Every cubic polyhedron has a Hamiltonian cycle through all its vertices”. Cubic means that three edges meet at every vertex. Without the cubic requirement, there are smaller polyhedra that are not Hamiltonian. The simplest counterexample is the rhombic dodecahedron. Every edge connects one of six valence-four vertices to one of eight valence-three vertices. The six valence-four vertices would need to occupy every other vertex in the length-14 tour. Six items cannot fill seven slots, so this is impossible.


Any noncubic graph can be made cubic by placing a small disk over the exceptions.


The word “polyhedral” implies that the graph must be 3-connected. If a line is drawn to disconnect the map, it must pass through at least three borders. Central Europe is not 3-connected, since a line through Spain will disconnect Portugal. France, the Vatican, and various islands also make the shape of Europe nonpolyhedral.


Tait’s method turns a Hamiltonian cycle on a cubic polyhedral graph into a four-coloring, by the following method.
- Alternately color the edges of the Hamiltonian cycle blue and purple. Color the other edges red.
- Throw out thin edges, and color the resulting polygon blue.
- Throw out dashed edges, and color the resulting polygon(s) red.
- Overlay the two colorings to get a four-coloring.


For 66 years, Tait’s conjecture held. In 1946, W. G. Tutte found the first counterexample, now known as Tutte’s graph. Since then, some smaller cubic polyhedral non-Hamiltonian graphs have been found, with the smallest such graph being the Barnette-Bosák-Lederberg graph, found in 1965. Seven years earlier, Lederberg had won the Nobel Prize in Medicine.


Hamilton-Connected Graphs
Hamilton’s Icosian game is unfortunately flawed. It is possible to choose two vertices that are not connected by a Hamiltonian path. An improvement would use a Hamilton-connected graph, where all pairs of vertices are connected by a Hamiltonian path [2]. A wide selection of these graphs is given by ![]() .
.


A more solving-friendly version of the 26-fullerene graph is given next [3]. Vertices have been replaced with squares, and edges are replaced by lines between neighboring squares or connecting green paths. A path at the edge of the diagram wraps around to the opposite edge. To try out the puzzle, put the letters A and Z in any two squares. Then try to find a connecting Hamiltonian path, using the letters A to Z. No matter where you put the A and Z, the puzzle is solvable. For example, if you started with A in block 2, and Z in block 6, one of the two solutions is (A)2 3 4 8 7 15 16 9 10 5 1 14 13 26 25 24 21 20 19 23 22 17 18 11 12 6(Z).

This path can be found and displayed with Mathematica, using the trick of adding a nondisplayed vertex connecting 2 to 6.

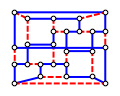
A harder puzzle involves the Coxeter graph minus an edge. Here is a solving-friendly version of this Hamiltonian puzzle.

References
| [1] | J. Dalgety. “The Icosian Game.” (Jul 6, 2009) puzzlemuseum.com/month/picm02/200207icosian.htm. |
| [2] | E. W. Weisstein. “Hamilton-Connected Graph” from Wolfram MathWorld—A Wolfram Web Resource. mathworld.wolfram.com/Hamilton-ConnectedGraph.html. |
| [3] | J. Tierney. “The Hamiltonian Puzzle.” (May 4, 2009) tierneylab.blogs.nytimes.com/2009/05/04/the-hamiltonian-puzzle. |
| Ed Pegg Jr, “The Icosian Game, Revisited,” The Mathematica Journal, 2010. dx.doi.org/doi:10.3888/tmj.11.3-1. | |
About the Author
Ed Pegg Jr
Scientific Information Editor
Wolfram Research, Inc.
edp@wolfram.com