Given a finite vertex set, one can construct every connected spanning hypergraph by first choosing a spanning hypertree, then choosing a blob on each of its edges.
Introduction
If ![]() is a finite vertex set and
is a finite vertex set and ![]() is a collection of finite subsets (called edges), none of which is a subset of another, we recursively define the swell of
is a collection of finite subsets (called edges), none of which is a subset of another, we recursively define the swell of ![]() ,
, ![]() , to be the collection of all sets that either:
, to be the collection of all sets that either:
- belong to

- are the union of some pair of overlapping sets, both already belonging to

For example, if
![]()
then
![]()
If we also have ![]() , then the set system
, then the set system ![]() is called a clutter. This condition means that (except in the case
is called a clutter. This condition means that (except in the case ![]() ) each edge contains at least two vertices, and the hypergraph spanned by the edge set is connected. Here the hypergraph
) each edge contains at least two vertices, and the hypergraph spanned by the edge set is connected. Here the hypergraph ![]() spanned by a set of edges
spanned by a set of edges ![]() is defined to have vertex set
is defined to have vertex set ![]() and edge set
and edge set ![]() . (There is no agreed-upon definition of “hypergraph.” For some authors it is any set system; for others it is a simplicial complex; for others it is an antichain of sets.)
. (There is no agreed-upon definition of “hypergraph.” For some authors it is any set system; for others it is a simplicial complex; for others it is an antichain of sets.)

![]()
![]()

![]()
![]()
![]()
![]()
Here is a larger clutter.
![]()

The number of clutters ![]() spanning
spanning ![]() vertices is given by A048143 (oeis.org/A048143),
vertices is given by A048143 (oeis.org/A048143),
![]()
This sequence varies as ![]() , so the number of digits required roughly doubles with each consecutive term. Our main example is just one of some 56 sextillion members of
, so the number of digits required roughly doubles with each consecutive term. Our main example is just one of some 56 sextillion members of ![]() .
.

![]()
![]()
![]()
![]()
This normalizing function is a universal invariant for the species of labeled clutters, meaning two clutters are isomorphic iff they have the same image.
![]()
![]()
Here is a list of nonisomorphic representatives for all clutters with up to four vertices, corresponding to “unlabeled” clutters. This brute-force enumeration may not work for ![]() .
.

![]()

Kernels and Caps in Clutters
A kernel of ![]() is a clutter
is a clutter ![]() (the restriction of
(the restriction of ![]() to edges that are subsets of
to edges that are subsets of ![]() ) for some
) for some ![]() .
.
![]()
![]()

Define ![]() .
.
A set partition ![]() is a set of disjoint sets with
is a set of disjoint sets with ![]() .
.
Suppose ![]() is a set partition of
is a set partition of ![]() such that each block
such that each block ![]() is a kernel of
is a kernel of ![]() (i.e.
(i.e. ![]() and
and ![]() ). Since
). Since ![]() would imply
would imply ![]() , it follows that the set of unions
, it follows that the set of unions ![]() is itself a clutter, which we call a cap of
is itself a clutter, which we call a cap of ![]() .
.
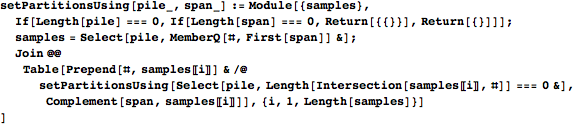
![]()
Equivalently, a cap ![]() of
of ![]() is a clutter satisfying both:
is a clutter satisfying both:
-

- every edge of
 is a subset of exactly one edge of
is a subset of exactly one edge of 
![]()
![]()

To see that this does not establish a partial order of clutters with a vertex set, observe that
is a nontransitive chain of caps. The following is the set of all set partitions of the edge set indices corresponding to each cap of the clutter.
![]()


In these plots of clutter partitions, the filled squares correspond to all pairs of a vertex and an edge such that the vertex belongs to the edge; these squares are then shaded according to which block of the partition the edge belongs to.
![]()

Trees and Blobs
The density of a clutter ![]() is
is
![]()
where the sum is over all edges ![]() .
.
![]()
A clutter ![]() with two or more edges is a tree iff
with two or more edges is a tree iff ![]() . This is equivalent to the usual definition of a spanning hypertree [1].
. This is equivalent to the usual definition of a spanning hypertree [1].
![]()
A clutter ![]() is a blob iff no cap of
is a blob iff no cap of ![]() is a tree.
is a tree.
![]()
The trees and blobs among the caps and kernels (respectively) of our running example are as follows.
![]()
![]()
![]()
![]()
Suppose a clutter ![]() decomposes into a cap
decomposes into a cap ![]() and corresponding set of kernels
and corresponding set of kernels ![]() . Then
. Then
![]()
where the sum is over all ![]() . In particular,
. In particular, ![]() , and
, and ![]() iff every
iff every ![]() is a tree. Using this simple identity, one easily proves the following.
is a tree. Using this simple identity, one easily proves the following.
Lemma
The following is also straightforward.
Proposition
We now come to the main result.
![]()
![]()
For our running example, the theorem corresponds to the following decomposition into a tree of blobs.
![]()
![]()
![]()
![]()
Theorem
Proof
First we show that any blob (kernel) is contained within a single branch of any tree (cap). Suppose that ![]() is a kernel of
is a kernel of ![]() and is a blob, and that
and is a blob, and that ![]() is a cap of
is a cap of ![]() that is a tree. Let
that is a tree. Let ![]() be the subtree of
be the subtree of ![]() contributing to the set partition
contributing to the set partition ![]() of non-empty intersections
of non-empty intersections ![]() for each branch
for each branch ![]() . The set of unions
. The set of unions ![]() forms a clutter that is obtained from
forms a clutter that is obtained from ![]() by deleting in turn all vertices not in
by deleting in turn all vertices not in ![]() , a process that weakly decreases density. Let
, a process that weakly decreases density. Let ![]() be the set partition comprised of maximal kernels (i.e. connected components) contained in blocks of
be the set partition comprised of maximal kernels (i.e. connected components) contained in blocks of ![]() . Then
. Then ![]() is a cap of
is a cap of ![]() and
and ![]() . Since
. Since ![]() is a connected clutter, we have
is a connected clutter, we have ![]() , and therefore
, and therefore ![]() . But since
. But since ![]() is a blob,
is a blob, ![]() cannot be a tree, hence it must be a maximal cap (viz.
cannot be a tree, hence it must be a maximal cap (viz. ![]() ,
, ![]() ).
).
Next we show that ![]() . If any two blobs overlap, both blobs must be contained entirely in whatever branch (of any given tree) contains their intersection. This implies that there is another blob containing their union, and hence that the maximal blobs
. If any two blobs overlap, both blobs must be contained entirely in whatever branch (of any given tree) contains their intersection. This implies that there is another blob containing their union, and hence that the maximal blobs ![]() are disjoint. Since every singleton is also a blob, we conclude that
are disjoint. Since every singleton is also a blob, we conclude that ![]() is a cap of
is a cap of ![]() .
.
Finally, if any kernel of ![]() were a blob, so would be the restriction of
were a blob, so would be the restriction of ![]() to its union, contradicting maximality of
to its union, contradicting maximality of ![]() . This proves that the set of unions of
. This proves that the set of unions of ![]() is a tree. ■
is a tree. ■
The following are the decompositions ![]() for each nonisomorphic clutter
for each nonisomorphic clutter ![]() with four vertices.
with four vertices.
![]()


Connected Sets of Kernels
Let ![]() be the set of all kernels of
be the set of all kernels of ![]() . If
. If ![]() is itself a (connected) clutter with vertex set
is itself a (connected) clutter with vertex set ![]() , then there exists a unique subset-minimal upper bound
, then there exists a unique subset-minimal upper bound ![]() satisfying both
satisfying both
-

 for all
for all 
In general, we can only define ![]() uniquely for
uniquely for ![]() a connected set of kernels, so
a connected set of kernels, so ![]() is not strictly a join operation for the poset of subsets
is not strictly a join operation for the poset of subsets ![]() . But if
. But if ![]() is not connected as a clutter, then letting
is not connected as a clutter, then letting ![]() be its (maximal) connected components, we say that
be its (maximal) connected components, we say that ![]() is a connected set of kernels iff
is a connected set of kernels iff ![]() is connected as a set of kernels, in which case the join is given by
is connected as a set of kernels, in which case the join is given by
![]()
In practice, the verification of connectedness and the computation of ![]() may require several iterations constructing joins of connected components. For example, consider the connected set of kernels.
may require several iterations constructing joins of connected components. For example, consider the connected set of kernels.
![]()
It has the following sequence of joins of connected components.



One Problem
If ![]() is a connected set of kernels, we define its compression
is a connected set of kernels, we define its compression ![]() to be the number of iterations in the computation of
to be the number of iterations in the computation of ![]() by constructing consecutive joins of connected components. For the previous example, we have
by constructing consecutive joins of connected components. For the previous example, we have ![]() . Although it seems unlikely that
. Although it seems unlikely that ![]() is a bounded invariant, we do not know how to construct an example with compression greater than
is a bounded invariant, we do not know how to construct an example with compression greater than ![]() .
.
- For which positive numbers
 does there exist a connected set of kernels
does there exist a connected set of kernels  such that
such that  ?
? - Does there exist an infinite chain
 of connected sets of kernels such that
of connected sets of kernels such that  for all
for all  ?
?
Define an invariant ![]() by
by
![]()
for all ![]() , where the sum is over all clutter partitions
, where the sum is over all clutter partitions ![]() . Here
. Here ![]() denotes the indicator function for a proposition
denotes the indicator function for a proposition ![]() , equal to 1 or 0 depending on whether
, equal to 1 or 0 depending on whether ![]() is true or false, respectively.
is true or false, respectively.
![]()
![]()
![]()
![]()
![]()
Theorem
Proof
Let ![]() be the set of all clutter partitions
be the set of all clutter partitions ![]() . What we have essentially shown above is that
. What we have essentially shown above is that ![]() , regarded as a subposet of the lattice of set partitions ordered by refinement, is a lattice. We have the simple enumerative identity
, regarded as a subposet of the lattice of set partitions ordered by refinement, is a lattice. We have the simple enumerative identity
![]()
where the product is over all non-singleton kernels ![]() , here regarded as elements of
, here regarded as elements of ![]() whose only non-singleton block is
whose only non-singleton block is ![]() . Expanding the right-hand side gives
. Expanding the right-hand side gives
![]()
where the sum is over all sets of non-singleton kernels ![]() , again regarded as lattice elements. Here
, again regarded as lattice elements. Here ![]() is algorithmically the same operation as the connected-join operation on
is algorithmically the same operation as the connected-join operation on ![]() . Expanding and factoring accordingly, this becomes
. Expanding and factoring accordingly, this becomes
![]()
where the outer sum is over all ![]() , the product is over all
, the product is over all ![]() , and the inner sum is over all connected sets of kernels
, and the inner sum is over all connected sets of kernels ![]() spanning
spanning ![]() . For any kernel
. For any kernel ![]() , define
, define
![]()
where the outer sum is over all clutter partitions ![]() , and where the product and inner sum are as before. Letting
, and where the product and inner sum are as before. Letting ![]() be the set partition of
be the set partition of ![]() whose only non-singleton block is
whose only non-singleton block is ![]() , we have shown that
, we have shown that
![]()
Hence our theorized expansion does indeed satisfy the defining identity of ![]() . ■
. ■
Note that it is sufficient in the preceding theorem and proof to consider only connected sets of subset-minimal non-singleton kernels, and it is often practical to do so. The hypergraph ![]() whose edges are minimal non-singleton kernels is also of some interest. The well-known Möbius function of a hypergraph is defined on the lattice of connected set partitions, and in this context an element of
whose edges are minimal non-singleton kernels is also of some interest. The well-known Möbius function of a hypergraph is defined on the lattice of connected set partitions, and in this context an element of ![]() may be called a pseudo-kernel. In comparison, however, our invariant
may be called a pseudo-kernel. In comparison, however, our invariant ![]() , which is defined on essentially all clutters, seems to be more interesting; we do not know if it has been studied before.
, which is defined on essentially all clutters, seems to be more interesting; we do not know if it has been studied before.
![]()
![]()
Additional Considerations
A semi-clutter is any anti-chain of subsets ![]() . For each finite set
. For each finite set ![]() , let
, let ![]() be the set of semi-clutters spanning
be the set of semi-clutters spanning ![]() . A species [2] is an endofunctor on the category of finite sets and bijections, so here we have defined a species of semi-clutters. The compound semi-clutter of a decomposition
. A species [2] is an endofunctor on the category of finite sets and bijections, so here we have defined a species of semi-clutters. The compound semi-clutter of a decomposition ![]() , as defined by Billera [3], is obtained as a disjoint “sum” of Cartesian “products.” Interpreted in the language of species theory, this is a certain natural transformation
, as defined by Billera [3], is obtained as a disjoint “sum” of Cartesian “products.” Interpreted in the language of species theory, this is a certain natural transformation
![]()
where ![]() denotes the composition operation on species, a generalization of composition of exponential formal power series. Let
denotes the composition operation on species, a generalization of composition of exponential formal power series. Let ![]() be the set of (connected) clutters spanning
be the set of (connected) clutters spanning ![]() , let
, let ![]() be the set
be the set ![]() containing only the maximal clutter on
containing only the maximal clutter on ![]() , and let
, and let ![]() be the set of clutters having no expression as a compound of a proper decomposition (i.e.
be the set of clutters having no expression as a compound of a proper decomposition (i.e. ![]() is the species of “prime” clutters). Billera’s main theorem (attributed to Shapley) establishes a unique reduced compound representation, which is itself a species of decompositions
is the species of “prime” clutters). Billera’s main theorem (attributed to Shapley) establishes a unique reduced compound representation, which is itself a species of decompositions
![]()
From this it is evident that ![]() can ultimately be reduced to a nested compound expression using only trivial and prime clutters. Hence the problem of enumerating semi-clutters on a vertex set is reduced to the problem of constructing, for any connected clutter, its “maximal proper committees,” which is the nontrivial solution of [2] for the enumeration of prime clutters considered. This is a particularly interesting application of formal species.
can ultimately be reduced to a nested compound expression using only trivial and prime clutters. Hence the problem of enumerating semi-clutters on a vertex set is reduced to the problem of constructing, for any connected clutter, its “maximal proper committees,” which is the nontrivial solution of [2] for the enumeration of prime clutters considered. This is a particularly interesting application of formal species.
References
| [1] | R. Bacher, “On the Enumeration of Labelled Hypertrees and of Labelled Bipartite Trees.” arxiv.org/abs/1102.2708. |
| [2] | A. Joyal, “Une théorie combinatoire des séries formelles,” Advances in Mathematics, 42(1), 1981 pp. 1–82. doi:10.1016/0001-8708(81)90052-9. |
| [3] | L. J. Billera, “On the Composition and Decomposition of Clutters,” Journal of Combinatorial Theory, Series B, 11(3), 1971 pp. 234–245. doi:10.1016/0095-8956(71)90033-5. |
| G. Wiseman, “Every Clutter Is a Tree of Blobs,” The Mathematica Journal, 2017. dx.doi.org/doi:10.3888/tmj.19-7. | |
About the Author
The author is a former graduate student of pure mathematics at the University of California, Davis. He is interested in categorical technology applied to discrete mathematics.
Gus Wiseman
gus@nafindix.com