We show how to use the Edgeworth series to construct an accurate approximation to the sampling distribution of the maximum likelihood estimator of a parameter of a Cauchy distribution. We then demonstrate the accuracy of this approximation, valid even for relatively small samples.

Introduction

Random variables in statistics have many different distributions; one of them is called Cauchy, and has the following probability density function:

(1)

where can have any real value. The distribution has two parameters and , which represent its median (the “location” parameter) and semi-interquartile deviation (the “scale” parameter), respectively. This rather unusual distribution has no mean and infinite standard deviation.

The exact parameter values are usually not known, and need to be estimated by repeating the corresponding random experiment independently times, and converting the information thus gathered into two respective estimates of and . The best way of doing this is by maximizing the corresponding likelihood function:

(2)

where the are the individual observations, or, equivalently, its logarithm

(3)

The maximization is usually achieved by setting the first derivative (with respect to each parameter) of the previous expression to zero, thus obtaining the so-called normal equations, namely

(4)

and

(5)

where the implicit solution (these equations cannot be solved explicitly for and ) defines the maximum likelihood (ML) estimators of and , denoted and , respectively. Since these estimators are always implicit functions of the random observations, they are both random variables, with their own distribution called the sampling distribution.

The normal equations can be rewritten more elegantly as

(6)

and

(7)

where each bar indicates taking the corresponding sample average— now symbolically represents all observations.

Approximating Sampling Distribution of

To simplify our task, we assume that the value of is known and equal to zero. From now on, we are thus concerned with estimating only the scale parameter , based on the following simplified version of (7):

(8)

Furthermore, we can introduce the following so-called pivot

(9)

which reduces (8) to

(10)

where is a random independent sample from the Cauchy distribution with and the scale parameter equal to 1. It is thus obvious that (and its sampling distribution) will be free of .

We first expand as a power series in (a “smallness” parameter— indicates that its coefficient is proportional to ), thus:

(11)

The first term is 1 since the corresponding expansion of must start with —this is a general property of a maximum likelihood estimator. We then similarly expand the expression under the bar in (10).

Placing a bar over each term and then replacing every by , where stands for the corresponding expected value (a plain number), lets us solve for , , and [1]. Here stands for .

Cumulants

The next step is to compute the expected value, variance, and the next two cumulants of . We recall the definition of cumulants as coefficients of in the following expansion.

This tells us that the second and third cumulants are equal to and , respectively, but the fourth cumulant is , where denotes the corresponding central moment, that is,

(12)

and is the expected value of (which also happens to be the first cumulant).

To find these, we need a procedure for computing the expected value of expressions involving products and powers of all possible sample averages (our bars) in our previous expansion of . This is trivial for a single bar (its expected value is always zero), and relatively easy for a product of two or three bars (including powers, as a special case), since one can show that

(13)

and

(14)

For example,

(15)

and so on.

Things get more complicated when the overall power is four or higher (we need to go up to six). In such a case, we first need to find all partitions of , where the individual subsets must have at least two elements each. Thus, for example, having four terms, we either take all of them as a single subset or partition them into two pairs, such as —there are three ways of doing this. Similarly, having six , we can either take all of them or split them into two triplets (10 ways), a pair and a quadruplet (15 ways), or three pairs (15 ways).

The contribution of each of these partitions is then computed using the following scheme: we multiply the expected values of the product of the in each subset, multiply the answer by , where is the number of these subsets, and divide by Thus, for example the partition contributes

(16)

To find, for example, , all such contributions from all corresponding partitions must be added together. This is done by the following program.

The second argument of EV specifies the accuracy to be achieved (up to when the argument is equal to 1, up to when it is equal to 2, etc.). At this point, becomes a redundant parameter and is eliminated by setting it to 1.

We can thus get the expected value, variance, and the next two cumulants of .

Edgeworth Expansion

One can show [2] that a good approximation to the probability density function of

(17)

is provided by

(18)

where and are the normalized cumulants, and are simple polynomials defined by

(19)

These are closely related to Hermite polynomials; the exact correspondence is clear from the first command.

The resulting expression can be easily transformed into a probability density function of , which can then be plotted for , for example.

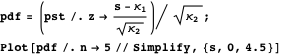
Comparison with Empirical Distribution

The best way of verifying the accuracy of this approximation is to generate a large collection of random independent samples of size five from a Cauchy distribution (with the location and scale parameters equal to 0 and 1, respectively), for each such sample compute the value of by solving (10), and then display these -values in a histogram.

We are now in a position to check how well our approximate probability density function, correspondingly rescaled, matches this histogram (which, for large total frequency, represents—up to small statistical fluctuations—the exact distribution of ).

Even though this is an improvement over the usual normal approximation, it is still far from a reasonably good match (but one should remember that five is an extremely small sample size—things do improve, rather dramatically, as increases).

Nevertheless, there is one particular technique one can employ to achieve a substantially better agreement, even with the current value of .

Transforming

We can use the same approach and program to find an approximation for the distribution of , where is an arbitrary (preferably increasing) function of a non-negative argument. This can be achieved by defining T and computing its first four cumulants.

The third cumulant can be thus made equal to zero for any by solving the following differential equation.

The simplest nontrivial solution is clear.

Now, we have to recompute the first four cumulants of .

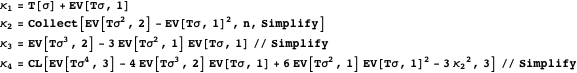
Having reduced to zero not only greatly simplifies the approximate probability density function of

(20)

but it also makes the corresponding approximation substantially more accurate.

This is now the new approximate probability density function.

The improvement can be seen by converting the previous probability density function of (20) to that
of .

Let us now compare the last function to the original histogram.

This has now produced a rather respectable agreement between the new approximation and the exact distribution.

Potential Extensions

In a similar manner, one can construct an approximate joint probability density function for both and . This requires the corresponding generalization of cumulants, Hermite polynomials, and the Edgeworth expansion. Readers with enough statistical expertise should have no difficulty pursuing that direction on their own since, surprisingly, the required modifications of the program presented in this article would not be that substantial. The most difficult part, namely the routine for computing the expected value of products and powers of sample averages, needs no change at all.

The same technique can also be used to find a good approximation to a probability density function of almost any parameter estimator of a specific distribution.

References

[1]	D. F. Andrews and J. E. Stafford, Symbolic Computation for Statistical Inference, New York: Oxford University Press, 2000.
[2]	F. Y. Edgeworth, “The Law of Error,” Transactions of the Cambridge Philosophical Society, 20, 1905 pp. 36-66 and 113-141. books.google.com/books/about/ Transactions_of_the _Cambridge _Philosophi.html?id=uTs8AAAAMAAJ.
J. Vrbik, “Sampling Distribution of ML Estimators: Cauchy Example,” The Mathematica Journal, 2011. dx.doi.org/doi:10.3888/tmj.13-19.

About the Author

Jan Vrbik
Department of Mathematics, Brock University
500 Glenridge Ave., St. Catharines
Ontario, Canada, L2S 3A1
jvrbik@brocku.ca