This article considers the acoustic field propagating in the radiation-dominated (![]() ) universe of arbitrary space curvature (
) universe of arbitrary space curvature (![]() ). The field equations are reduced to the d’Alembert equation in an auxiliary static Robertson-Walker spacetime and dispersion relations are discussed.
). The field equations are reduced to the d’Alembert equation in an auxiliary static Robertson-Walker spacetime and dispersion relations are discussed.
Introduction
The Sachs-Wolfe theorem ([1], pp. 76-77) contains two separate results formulated for two different equations of state: the first (i, p. 76) for pressureless matter (![]() ) and the second (ii, p. 77) for an ultrarelativistic gas (
) and the second (ii, p. 77) for an ultrarelativistic gas (![]() ). The first result was recently recalculated and discussed in [2]. In this article we concentrate on the latter and call it the acoustic theorem to distinguish it from the former.
). The first result was recently recalculated and discussed in [2]. In this article we concentrate on the latter and call it the acoustic theorem to distinguish it from the former.
The acoustic theorem refers to the spatially flat (![]() ), hot (
), hot (![]() ) Friedmann-Robertson-Walker universe and the scalar perturbation propagating in it. The theorem states that with the appropriate choice of the perturbation variable, one can express the propagation equation in the form of d’Alembert’s equation in Minkowski spacetime. Scalar perturbations in the flat, early universe propagate like electromagnetic or gravitational waves ([1], p. 79; see also [3]).
) Friedmann-Robertson-Walker universe and the scalar perturbation propagating in it. The theorem states that with the appropriate choice of the perturbation variable, one can express the propagation equation in the form of d’Alembert’s equation in Minkowski spacetime. Scalar perturbations in the flat, early universe propagate like electromagnetic or gravitational waves ([1], p. 79; see also [3]).
On the other hand, the wave equation for the scalar field of the dust (![]() ) cosmological model can be transformed into the d’Alembert equation in the static Robertson-Walker spacetime, regardless of the universe’s space curvature (see [4]). Therefore, we can suppose that the flatness assumption in the Sachs-Wolfe theorem is not needed and that the theorem is true in the general case. The proof of this fact, formulated as a symbolic computation, is the subject of this article.
) cosmological model can be transformed into the d’Alembert equation in the static Robertson-Walker spacetime, regardless of the universe’s space curvature (see [4]). Therefore, we can suppose that the flatness assumption in the Sachs-Wolfe theorem is not needed and that the theorem is true in the general case. The proof of this fact, formulated as a symbolic computation, is the subject of this article.
We have found the synchronous coordinate system the most convenient for algorithmic purposes. The code is concise and does not involve concepts other than those covered in classical papers and textbooks [1, 5, 6]. The perturbation equations can also be reduced to d’Alembert’s equation in other gauge-invariant formalisms [7]. The level of difficulty depends on the formalism, but in each case difficulties are computational rather than conceptual.
Originally, the Sachs-Wolfe theorem was published without a detailed proof. The theorem contradicts the heuristic, but popular Jeans instability criterion (instability is not the best word; gravitational and electromagnetic waves show the same kind of behavior [1, p. 79]). Probably these two circumstances are responsible for the Jeans instability criterion’s still playing a marginal role in explaining cosmic microwave background radiation fluctuations [8] and cosmological structure genesis.
This article consists of a brief description of the problem and a short verification using Mathematica. Throughout, ![]() and
and ![]() .
.
Scalar Perturbations on the Friedmann-Robertson-Walker Background
We adopt Robertson-Walker metrics in spherical coordinates ![]() :
:
 |
(1) |
with the scale factor ![]() appropriate for the equation of state
appropriate for the equation of state ![]() ,
,
| (2) |
Consider the scalar perturbations in the synchronous system of reference. The metric tensor correction is then determined by two scalar functions ![]() and
and ![]() [9]:
[9]:
| (3) |
| (4) |
Here ![]() stands for the Beltrami-Laplace operator on the
stands for the Beltrami-Laplace operator on the ![]() hypersurface. Eventually, the metric takes the form
hypersurface. Eventually, the metric takes the form
| (5) |
To first order in the perturbation expansion, the Einstein equations with the metric tensor (5) reduce to
| (6) |
| (7) |
where we set ![]() ,
, ![]() (in agreement with [5, 6]);
(in agreement with [5, 6]); ![]() stands for sound velocity. The density contrast
stands for sound velocity. The density contrast ![]() reads
reads
| (8) |
Let us define a new perturbation variable ![]() with the help of the second-order differential transformation of the density contrast
with the help of the second-order differential transformation of the density contrast ![]() ,
,
| (9) |
The function ![]() is the solution of the d’Alembert equation
is the solution of the d’Alembert equation
| (10) |
with the Beltrami-Laplace operator ![]() acting in this space,
acting in this space,
 |
(11) |
Sachs-Wolfe Acoustic Theorem for ![]()
Proof
We perform this calculation in Mathematica. The commands are reproduced below and also can be downloaded from drac.oa.uj.edu.pl/usr/woszcz/kody/acoucticRWcode.nb.
Mathematica Verification
Coordinates

Friedmann-Robertson-Walker Background for 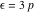

Lifshitz-Khalatnikov Perturbation Equations (Partial Differential Form)

The Density Contrast
![]()
Higher-Order Derivatives

Laplacian in the Maximally Symmetric Three-Dimensional Curved Space

The Gauge-Invariant Variable 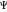

The Wave Equation
![]()
![]()
![]()
Dispersion Relations
Equation (10) reduces the problem of cosmological density perturbations to a field theory on a curved background (see [10]). Acoustic waves are dispersed by the space curvature. The dispersion relation for equation (10) takes the form ([10] equation (5.27))
| (12) |
and the group velocity becomes
| (13) |
In flat space (![]() ), the group velocity is constant and equal to
), the group velocity is constant and equal to ![]() . For
. For ![]() , the dispersion relation is nonlinear. In a space of negative curvature (
, the dispersion relation is nonlinear. In a space of negative curvature (![]() ), the waves behave as a scalar field with mass
), the waves behave as a scalar field with mass ![]() . The group velocity is a function of
. The group velocity is a function of ![]() and decreases to zero in the limit as
and decreases to zero in the limit as ![]() ,
,
| (14) |
while the limit frequency is still positive
| (15) |
Acoustic behavior does not extend to the solutions for imaginary ![]() such that
such that ![]() (supplementary series [11, 12], supercurvature modes [13]).
(supplementary series [11, 12], supercurvature modes [13]).
In a closed universe (![]() ), the wave numbers are integers and
), the wave numbers are integers and ![]() . The general solution is a countable combination of hyperspherical functions.
. The general solution is a countable combination of hyperspherical functions.
Using the basis functions ![]() , one can reconstruct the solution for the density fraction
, one can reconstruct the solution for the density fraction ![]() by means of the reciprocal relation (9). Compare the analogous procedure for the scalar field [4]. Reconstructing
by means of the reciprocal relation (9). Compare the analogous procedure for the scalar field [4]. Reconstructing ![]() makes it necessary to restore the less desirable gauge ambiguity.
makes it necessary to restore the less desirable gauge ambiguity.
Conclusion
A generic solution to equation (10) forms a random wave field in some auxiliary static Robertson-Walker spacetime. The space curvature ![]() is the only quantity that affects the wave dispersion. Neither the Jeans scale nor the horizon size appears in equation (10); consequently, the dispersion relation (12) does not indicate them as critical values. Critical scales of the Jeans type, which emerge in some Newtonian approaches, disappear in a fully relativistic treatment. Equation (10) does not confirm the existence of frozen modes [14]. The waves, whether inside or outside the horizon, propagate in the same manner (for
is the only quantity that affects the wave dispersion. Neither the Jeans scale nor the horizon size appears in equation (10); consequently, the dispersion relation (12) does not indicate them as critical values. Critical scales of the Jeans type, which emerge in some Newtonian approaches, disappear in a fully relativistic treatment. Equation (10) does not confirm the existence of frozen modes [14]. The waves, whether inside or outside the horizon, propagate in the same manner (for ![]() with the same phase and group velocity), and do not change at the horizon crossing. Frozen modes (implemented in cosmological software [15]) involved in deciphering cosmological parameters [8] are not solutions consistent with general relativity.
with the same phase and group velocity), and do not change at the horizon crossing. Frozen modes (implemented in cosmological software [15]) involved in deciphering cosmological parameters [8] are not solutions consistent with general relativity.
A further consequence of the Sachs-Wolfe acoustic theorem is that the canonical formalism is adequate to define the constants of motion for a scalar perturbations field. For ![]() , the construction of conserved quantities (energy, momentum, and angular momentum) is fairly obvious and reproduces that from other scalar fields in Minkowski space [10]. For
, the construction of conserved quantities (energy, momentum, and angular momentum) is fairly obvious and reproduces that from other scalar fields in Minkowski space [10]. For ![]() , the hyperbolic momentum must be introduced and the Fourier expansion limited to the principal series of the Laplacian eigenfunctions.
, the hyperbolic momentum must be introduced and the Fourier expansion limited to the principal series of the Laplacian eigenfunctions.
References
| [1] | R. K. Sachs and A. M. Wolfe, “Perturbations of a Cosmological Model and Angular Variations of the Microwave Background,” The Astrophysical Journal, 147, 1967 pp. 73-90. doi: 10.1086/148982. |
| [2] | R. K. Sachs, A. M. Wolfe, G. Ellis, J. Ehlers, and A. Krasinski, “Perturbations of a Cosmological Model and Angular Variations of the Microwave Background,” General Relativity and Gravitation, 39, 2007 pp. 1929-1961. doi: 10.1007/s10714-007-0448-9. |
| [3] | L. P. Grishchuk, “Discovering Relic Gravitational Waves in Cosmic Microwave Background Radiation.” arxiv:0707.3319v4. |
| [4] | S. Klainerman and P. Sarnak, “Explicit Solutions of |
| [5] | E. M. Lifshitz and I. M. Khalatnikov, “Investigations in Relativistic Cosmology,” Advances in Physics, 12, 1963 pp. 185-249. doi: 10.1080/00018736300101283. |
| [6] | L. D. Landau and E. M. Lifshitz, The Classical Theory of Fields: Course of Theoretical Physics, Vol. 2, 4th ed., Oxford: Butterworth-Heinemann (Elsevier), 2000. |
| [7] | Z. A. Golda and A. Woszczyna, “A Field Theory Approach to Cosmological Density Perturbations,” Physics Letters A, 310(5), 2003 pp. 357-362. doi: 10.1016/S0375-9601(03)00380-3. |
| [8] | D. N. Spergel, L. Verde, H. V. Peiris, E. Komatsu, M. R. Nolta, C. L. Bennett, M. Halpern, G. Hinshaw, N. Jarosik, A. Kogut, M. Limon, S. S. Meyer, L. Page, G. S. Tucker, J. L. Weiland, E. Wollack, and E. L. Wright, “First-Year Wilkinson Microwave Anistropy Probe (WMAP) Observations: Determination of Cosmological Parameters,” The Astrophysical Journal Supplement Series, 148(1), 2003 pp. 175-194. doi: 10.1086/377226. |
| [9] | J. M. Stewart, “Perturbations of Friedmann-Robertson-Walker Cosmological Models,” Classical and Quantum Gravity, 7(7), 1990 pp. 1169-1180. doi: 10.1088/0264-9381/7/7/013. |
| [10] | N. D. Birrell and P. C. W. Davies, Quantum Fields in Curved Space, New York: Cambridge University Press, 1982. |
| [11] | I. M. Gelfand, M. I. Graev, and N. Ya. Vilenkin, Generalized Functions, Vol. 5: Integral Geometry and Representation Theory, New York: Academic Press Inc., 1966. |
| [12] | M. A. Naimark, Linear Representations of the Lorentz Group, Oxford: Pergamon, 1964. |
| [13] | D. H. Lyth and A. Woszczyna, “Large Scale Perturbations in the Open Universe,” Physical Review D, 52(6), 1995 pp. 3338-3357. doi: 10.1103/PhysRevD.52.3338. |
| [14] | M. White and J. D. Cohn, “Resource Letter: TACMB-1: The Theory of Anisotropies in the Cosmic Microwave Background,” American Journal of Physics, 70(2), 2002 p. 106. arxiv:astro-ph/0203120v1. |
| [15] | U. Seljak and M. Zaldarriaga, “A Line of Sight Approach to Cosmic Microwave Background Anisotropies,” The Astrophysical Journal Supplement, 469, 1996 pp. 437-444. arxiv.org/abs/astro-ph/9603033. |
| W. Czaja, Z. A. Golda, and A. Woszczyna, “The Acoustic Wave Equation in the Expanding Universe: Sachs-Wolfe Theorem,” The Mathematica Journal, 2011. dx.doi.org/doi:10.3888/tmj.13-18. | |
About the Authors
Wojciech Czaja
Copernicus Center for Interdisciplinary Studies
ul. Sławkowska 17
31-016 Kraków, Poland
W.Czaja@oa.uj.edu.pl
Zdzisław A. Golda
Jagiellonian University, The Faculty of Physics, Astronomy and Applied Computer Science
ul. Orla 171
30-244 Kraków, Poland
and
Copernicus Center for Interdisciplinary Studies
ul. Sławkowska 17
31-016 Kraków, Poland
zdzislaw.golda@uj.edu.pl
Andrzej Woszczyna
Jagiellonian University, The Faculty of Physics, Astronomy and Applied Computer Science
ul. Orla 171
30-244 Kraków, Poland
and
Copernicus Center for Interdisciplinary Studies
ul. Sławkowska 17
31-016 Kraków, Poland
uowoszcz@cyf-kr.edu.pl