Volume 14

Fourier-space representation of the partial differential equations describing nonlinear dynamics of continuous media in cylindrical geometry can be achieved using Chandrasekhar-Kendall (C-K) functions defined over infinite domain as an orthogonal basis for solenoidal vector fields and their generating function and its gradient as orthogonal bases for scalar and irrotational vector fields, respectively. All differential and integral operations involved in translating the partial differential equations into transform space are then carried out on the basis functions, leaving a set of time evolution equations, which describe the rate of change of the spectral coefficient of an evolving mode in terms of an aggregate effect of pairs of interacting modes computed as an integral over a product of spectral coefficients of two physical quantities along with a kernel, which involves the following integral:

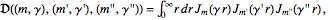
involving the product of three Bessel functions of the first kind of integer order. This article looks at this integral’s properties using a semi-empirical approach supported by numerical experiments. It is shown that this integral has well-characterized singular behavior. Significant reduction in computational complexity is possible using the proposed empirical approximation to this integral. Read More »

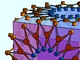
In this article we explore possible clusters of rhombic triacontahedra (RTs), usually by connecting them face to face, which happens when they are placed at the vertices of certain polyhedra. The edge length of such polyhedra is set to be twice the distance of a face of an RT from the origin (about 2.7527). The clusters thus produced can be used to build further clusters using an RT and a rhombic hexecontahedron (RH), the logo of Wolfram|Alpha. We briefly look at other kinds of connections and produce new clusters from old by using matching polyhedra instead of RTs. Read More »

We consider the problem of landing a spacecraft on the Moon, assuming that aerodynamic and gravitational forces of bodies other than the Moon are negligible, and lateral motion can be ignored. Accordingly, the descent trajectory is vertical, and the thrust vector is tangent to the trajectory.

Because the spacecraft is near the Moon, we assume that the lunar acceleration of gravity has the constant value , that the relative velocity of the exhaust gases with respect to the spacecraft is constant, and that the mass rate is constrained by , where is constant and gives the maximum rate of change of the mass due to burning the fuel.
Read More »

The special function (the Walker function) and its derivatives are important for the description of near-wall turbulent flows. This article gives exact expressions for these functions, based on original identities for the hypergeometric functions and . We also introduce a new initial value problem that generates interpolating functions for and its derivatives. Read More »

We introduce some key formulas of special relativity and apply them to the motion of a spinless, charged point particle of unit mass, subject to the Lorentz force due to an external electromagnetic field. Read More »

Using closure over a complete set of rotational states for methane to evaluate the intensity for quasi-elastic electron scattering in the first Born approximation, a number of integrals were encountered that appear not to have been evaluated previously. Mathematica was employed to evaluate these and similar integrals, and it was discovered that in all the cases studied the results could be represented by simple formulas. Read More »

Differential equation models for population dynamics are now standard fare in single-variable calculus. Building on these ordinary differential equation (ODE) models provides the opportunity for a meaningful and intuitive introduction to partial differential equations (PDEs). This article illustrates PDE models for location-dependent carrying capacities, migrations, and the dispersion of a population. The PDE models themselves are built from the logistic equation with location-dependent parameters, the traveling wave equation, and the diffusion equation. The approach presented here is suitable for a single lecture, reading assignment, and exercise set in multivariable calculus. Interactive examples accompany the text and the article is designed for use as a CDF document in which some of the input can remain hidden. Read More »

We develop symbolic methods of asymptotic approximations for solutions of linear ordinary differential equations and use them to stabilize numerical calculations. Our method follows classical analysis for first-order systems and higher-order scalar equations where growth behavior is expressed in terms of elementary functions. We then recast our equations in modified form, thereby obtaining stability. Read More »

We investigate the classical problem of a gambler repeatedly betting $1 on the flip of a potentially biased coin until he either loses all his money or wins the money of his opponent. This is then extended to the case of his adversary (a casino) having practically unlimited resources and used to derive the inverse Gaussian distribution of the first passage time. Read More »

This article describes how to model diffusion using NDSolve, and then compares that to constructing your own methods using procedural, functional, rule-based, and modular programming. While based on the diffusion equation, these techniques can be applied to any partial differential equation. Read More »